Abstract
Keywords
Cognitive Development Evolution Infancy Intelligence Spatial Behavior Rats
1. Introduction
In the core of his theory, Jean Piaget (1-3) proposed an adaptive role for acting on objects in the formation of logical constructs during development. Historically, Henri Poincaré, who had recognized the properties of mathematical groups in theoretical physics (4), proposed that such groups were innate constructs (5). Inspired by Poincare’s proposal, Piaget studied the mathematical properties of the “group of displacements” with respect to the structure of spatial behavior and concluded that these groups gradually form during infancy, demonstrating the existence of a pre-language logic in infants (2, 6).
Mathematically speaking, a group is a set including a number of members under binary operations that satisfies some axioms. For example, closure represents an axiom in which the two-by-two combinations of elements in the group will result in another member of the same group. There are other axioms, including identity, inverse, and associative properties (7). In explaining the psychological aspect of such “logico-mathematical” properties, Piaget (2) theorized the gradual formation of object permanence along with the construction of other entities such as space, time, and causality as infants organize their movements into the “group of displacements” (2, 6). An infant removes a cover to make an object reappear after it is hidden underneath the cover by the experimenter. This is an example of a behavior that represents a reverse action and corresponds to the property of inverse in the language of group theory. Identity, on the other hand, represents a condition in which no action takes place, and associative property can be inferred from the behavior of the infant when it solves a detour problem.
The effect of different variables on detour behaviors has been studied in human infants (8). Such behaviors have been reported in other species such as the chimpanzee or rat (Rattus Norvegicus) under experimental conditions (2, 9-11). Nevertheless, it is important to determine whether innate spatial behaviors (e.g., spontaneous exploration) also represent the same properties of mathematical groups. The present analysis will primarily focus on examining the correspondence between innate spatial exploration reported in rats (12-14) and the properties of mathematical groups.
2. Arguments
2.1. Exploration, Protection, and Navigational Mechanisms
Animals explore the environment to find food and try to return home without being exposed to predators (15-17). Systematic investigation of exploratory behavior in laboratories also confirms an innate tendency in rats to return to a (reportedly safer) starting position after each excursion in an exploratory bout (13, 14, 17, 18). In order to do so, they have to adopt patterns of exploration such as shortcuts (12, 13, 19) that may minimize the chance of being exposed to potential dangers instead of taking the same path as the one taken at the time of departure.
Thus, it should come as no surprise to us when we observe the emergence of navigational mechanisms that enhance the survival value of the behavior by making it easier and more effective for animals to return home or any starting point that perhaps serves as a safe place (17, 18). There are 2 mechanisms by which animals may return to the starting position. Animals may use ambient cues to return to the starting position via piloting or they may use movement-related cues and return to the starting position via dead reckoning (path integration) (13, 19). The latter kind of returns represents the ability of animals to make shortcuts (13).
Darwin (20) had written about dead reckoning as one of animals’ spatial ability long before Piaget spoke about infants’ ability to use alternative paths (2, 6). Dead reckoning was later modelled mathematically by a number of scientists (21). For instance, Mittelstaedt and Mittelstaedt (12) advanced a mathematical model to explain the behavior of animals based on path integration and proposed that animals compute the integrals of the sine and cosine for each rotation they make over their total path to update their position in a Cartesian coordinate system and to return home through the shortest possible route. The hippocampus and related brain areas play a critical role in such behaviors, and neuroscientists have developed models in which path integration is either a part or the very fundamental basis of spatial navigation (21-23).
2.2. Mathematical Structure of Exploratory Excursion by Rats
In addition to the mathematics that explains the return to the starting position by rats assuming their brain as a computational system (21), the structure of spatial behavior itself can be mathematically analyzed to serve different purposes. For example, Piaget’s main objective of his analysis was to demonstrate a form of pre-language logic in infants’ behavior (6). The ability to take an alternative path can be found both in rats and in human infants. Here, the analysis will be expanded to discuss the comparative status of spatial (shortcut) behavior in relation to the formation of abstract processes and cognitive competence.
When a rat makes an outward trip and returns to the starting position, the structure of such an excursion may correspond to some mathematical structures. For instance, if a rat returns to the starting position taking the reverse path of the one taken at the time of departure, which is usually on the edge of a circular table in the laboratory (14), the structure of the excursion would imply a reverse action that is an equivalent of inverse in the language of group theory. However, if a rat returns to the starting position using a more direct path–usually crossing the center of the table instead of the circuitous path taken during the outward trip (13, 14) such a behavior would indicate a shortcut and suggest that the pattern of the animal’s excursion is mathematically consistent with associative property.
A starting point to which rats return can be superimposed on the origin of a Cartesian coordinate system in which–for example–the tail of the first leg (Vector 1) and the tip of the second leg (Vector 2) of a 2-leg outward trip can be connected via a third leg (V1 + V2) as a result of a vector addition (Figure 1). In other words, the third vector (ie, shortcut) lands in the same vector space as the first 2 vectors do (the property of closure), and together they form a group of displacements (associative property).
Vector Addition, Shortcut, and Group
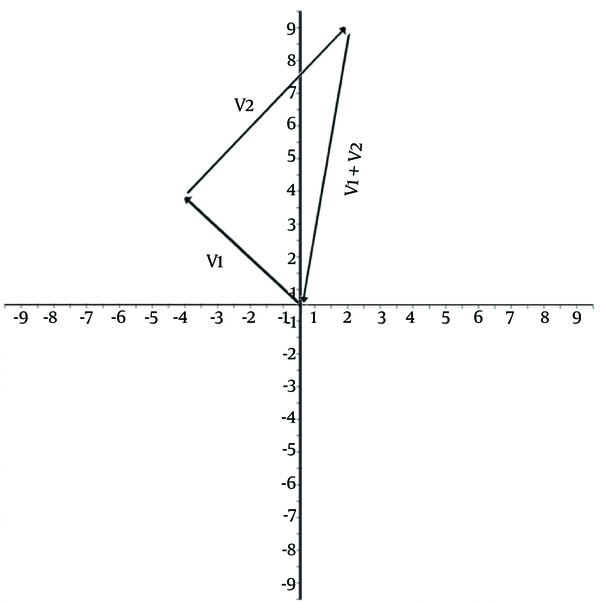
2.3. Rats Versus Humans: Differences in Spatial Behavior
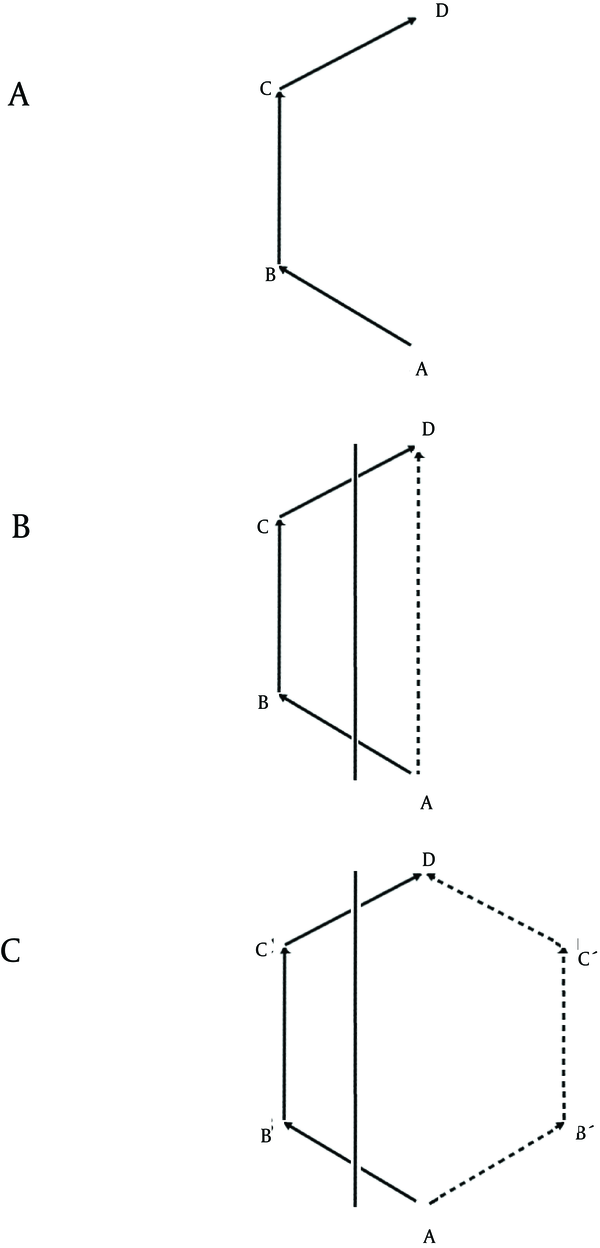
Although spatial behavior can be mathematically described in a parallel manner in humans and nonhumans, there are differences when one analyzes their performance. For example, humans and nonhumans (e.g., rats or mice) may use 1 or another path to get from A to D. They might choose path ABCD (Figure 2 a) or if path AB and/or CD are blocked, they may choose path AD (Figure 2 b), which represents a shortcut. Any other paths such as ABʹCʹD do not represent a shortcut (Figure 2 c).
Paths in an Exploration Task
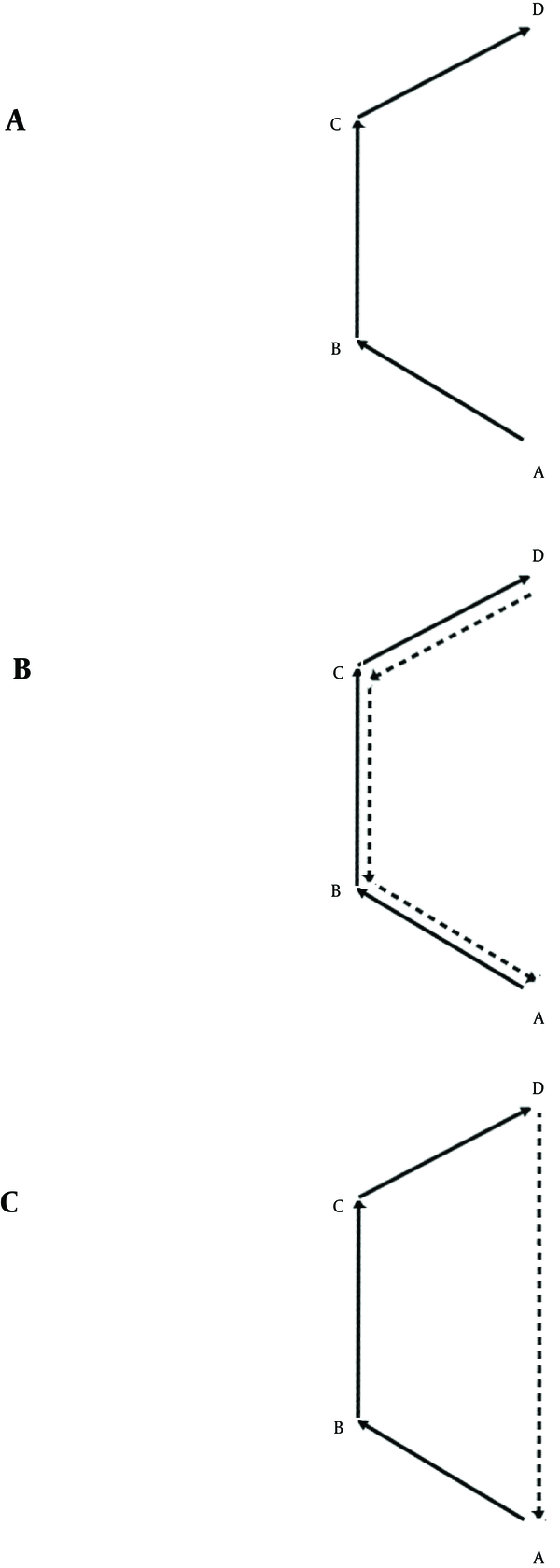
However, such spatial behavior in rats (or mice) seems to be qualitatively different from that in humans in the sense that rats return to their home base or to their point of entry in a predictable and repeating manner and without any training (14). Such visits are also associated with certain behaviors such as a disproportionate length and number of stops around the home base or the point of entry or other behaviors such as grooming (14, 18). In other words, when a rat chooses path ABCD to get from A to D (Figure 3 a), its return to-for example -the starting point may take the form of a reverse action (Figure 3 b) or a shortcut (Figure 3 c) to a place to which it has to return repeatedly. Such innately defined places to which rats are led to return by their navigational system have not been reported in human populations.
Path Finding as an Innate Behavior
2.4. Rats Versus Humans: Abstract Processes and Cognitive Competence
What is the implication of behavioral similarities or differences between rats and humans for their cognitive competence? One way of answering this question is to determine how such similarities and differences could be instrumental in theorizing human cognition. Since an essential element of cognition is the ability to extract constructs from particulars (abstraction) and generalize them to new cases (24, 25), the main focus should be on the role of the pre-language development of mathematically structured behavior in the process of abstraction in humans compared to that in animals.
In order to examine this role, we first need to see what can be basically extracted from more concrete items to form a more abstract level of a structure. Thus, it might be best to take a closer look at the evolution of abstract algebra itself. A careful examination of the history of algebra, from the time the term “algebra” (al jebr) was coined and later introduced to the world as the science of solving equations to this day of modern age, indicates that what has been abstracted to form today’s abstract algebra has been the general principles, which are common among different branches of algebra today (7).
By the same token, a closer look at the characteristics of-for example-a closed group reveals that the “logico-mathematical” correspondence can be observed not only at a behavioral level but also at a cognitive level in humans. For instance, not only does infants’ spatial behavior represent the properties of a closed system (2, 7), but also the same principle of closure is followed when humans deal with numbers (e.g., when 2 even numbers add up to another even number, of 7). This is a representative example of 2 levels of abstraction that follows the same rule. In other words, the same principles that are observable at the behavioral level (a less abstract entity) are represented at the cognitive level (a more abstract entity) during human development. Therefore, the importance of studying mathematical constructs inferred from behavior is due to the role that they may or may not play as common principles in the process of abstraction.
Thus, the present analysis raises new questions for comparative studies within the theoretical framework proposed by Piaget (1, 2, 6). The priority that Piaget granted to the role of action in the development of cognition and our ability to infer a parallel mathematical structure from the behavior of rodents or chimpanzees and human infants raise the question: “Why do other animals not possess the same level of cognitive competence compared to humans?” One answer might be that although both humans and-for example-rats demonstrate a certain degree of abstraction (26) and share the same mathematically structured behavior, there are differences as well. Automatic aspect of innate behavior and, therefore, less involvement in learning processes such as trials and errors by rats may have caused such limitations in their level of abstraction and cognitive competence.
3. Conclusions
In sum, as much as the parallel mathematical description of spatial behavior in rats and humans is consistent with the recent finding that low-frequency rhythms in the hippocampus are present in both species (27), it is important to note that such parallel structures (2, 14) cannot explain the difference in the cognitive capacities of the species. While species such as rats, mice, chimpanzees, and humans all share the same mathematical structure in their baseline spatial behaviors with arguably the same survival value, extraordinary cognitive capacity in humans indicates the possibility of a unique ability to abstract cognitive constructs from behavior. This clearly rules out the explanation that cognitive competence in humans is greater simply because other species lack a comparable baseline condition. In fact, it would be difficult to explain the crucial role of behavior in the formation of the evolutionary path as a result of a new form of natural selection dictated by the niche of the organism’s behavior (28). In other words, as long as we consider a crucial role for action in the formation of cognition, the uniqueness of human cognition remains unexplained.
The organization of movements is still considered central to the intellectual development during infancy; nevertheless, some experiments have questioned the degree to which innate movements play a role in cognition (29, 30). This implies that despite the parallel organization of the behavior, the difference in cognitive capacities among species may be theoretically explained based on other possibilities such as overestimation of the role of innate movements and/or underestimation of the role of language and other variables in cognitive development. Thus, although Piaget formulated the most dominant cognitive developmental theory, it may need a closer examination in terms of making universal statements to formulate a comparative view.
The difference in the performance and outcome between 2 species, despite the common mathematical description of their behavior, provides a supportive example in neurobiology for Kuhn’s (31) notion presented within the context of philosophy of physics in that 2 different phenomena may have parallel mathematical descriptions but whether they are the same always has to be examined at the conceptual level. This is consistent with the notion that abstract problems such as transitive inferences (or detour problem in the present study), which are behaviorally solved by rats, may not actually represent an operation in prepositional calculus as it is more likely to be the case with humans (32).
Finally, a rationale to account for such a gap in cognitive competence between humans and other species may be that a unique phylogenetic path has led to such an extraordinary cognitive competence in humans. A phylogenetic approach to comparative psychology may provide a better opportunity to investigate the diversity of cognitive status in species whose performance–for example–in some Piagetian tasks does not fit in any major phylogenetic grouping (33). Such studies would contribute to the fields of research such as neurology or psychiatry in which the validity of generalization from animal studies to human conditions is crucial.
References
-
1.
Piaget J. Psychology and Epistemology: Towards a theory of knowledge. New York: The Viking Press; 1971.
-
2.
Piaget J. Piercy DEB, editor. The Psychology of Intelligence. London: Routledge; 1950.
-
3.
Piaget J. Relations between psychology and other sciences. Annu Rev Psychol. 1979;30:1-8. [PubMed ID: 18771402]. https://doi.org/10.1146/annurev.ps.30.020179.000245.
-
4.
Darrigol O. The Genesis of the Theory of Relativity. 47. 2006. https://doi.org/10.1007/3-7643-7436-5_1.
-
5.
Poincaré H. Science and Hypothesis. reprint ed. Courier Corporation; 1952.
-
6.
Piaget J, Inhelder B. The psychology of the child. London: Basic Books; 1969.
-
7.
Pinter CH. A book of abstract algebra. New York: McGraw-Hill; 1982.
-
8.
Lockman JJ. The development of detour ability during infancy. Child Dev. 1984;55(2):482-91. [PubMed ID: 6723446].
-
9.
Chapuis N. Detour and Shortcut Abilities in Several Species of Mammals. Springer; 1987. https://doi.org/10.1007/978-94-009-3531-0_7.
-
10.
Chapuis N, Scardigli P. Shortcut ability in hamsters (Mesocricetus auratus): The role of environmental and kinesthetic information. Animal Learn Behav. 1993;21(3):255-65. https://doi.org/10.3758/bf03197990.
-
11.
Roberts WA, Cruz C, Tremblay J. Rats take correct novel routes and shortcuts in an enclosed maze. J Exp Psychol Anim Behav Process. 2007;33(2):79-91. [PubMed ID: 17469957]. https://doi.org/10.1037/0097-7403.33.2.79.
-
12.
Mittelstaedt H, Mittelstaedt ML. Homing by path integration. In: Papi F, Wallraff HG, editors. Avian navigation. New York: Springer; 1982.
-
13.
Wallace DG, Hines DJ, Whishaw IQ. Quantification of a single exploratory trip reveals hippocampal formation mediated dead reckoning. J Neurosci Meth. 2002;113(2):131-45. https://doi.org/10.1016/s0165-0270(01)00489-7.
-
14.
Nemati F, Whishaw IQ. The point of entry contributes to the organization of exploratory behavior of rats on an open field: an example of spontaneous episodic memory. Behav Brain Res. 2007;182(1):119-28. [PubMed ID: 17590451]. https://doi.org/10.1016/j.bbr.2007.05.016.
-
15.
Lima SL. Maximizing feeding efficiency and minimizing time exposed to predators: a trade-off in the black-capped chickadee. Oecologia. 1985;66(1):60-7. https://doi.org/10.1007/bf00378552.
-
16.
Lima SL, Valone TJ, Caraco T. Foraging-efficiency-predation-risk trade-off in the grey squirrel. Animal Behav. 1985;33(1):155-65. https://doi.org/10.1016/s0003-3472(85)80129-9.
-
17.
Whishaw IQ, Gharbawie OA, Clark BJ, Lehmann H. The exploratory behavior of rats in an open environment optimizes security. Behav Brain Res. 2006;171(2):230-9. [PubMed ID: 16678279]. https://doi.org/10.1016/j.bbr.2006.03.037.
-
18.
Hines DJ, Whishaw IQ. Home bases formed to visual cues but not to self-movement (dead reckoning) cues in exploring hippocampectomized rats. Eur J Neurosci. 2005;22(9):2363-75. [PubMed ID: 16262675]. https://doi.org/10.1111/j.1460-9568.2005.04412.x.
-
19.
Whishaw IQ, Hines DJ, Wallace DG. Dead reckoning (path integration) requires the hippocampal formation: evidence from spontaneous exploration and spatial learning tasks in light (allothetic) and dark (idiothetic) tests. Behav Brain Res. 2001;127(1-2):49-69. https://doi.org/10.1016/s0166-4328(01)00359-x.
-
20.
Darwin C. Origin of Certain Instincts. Nature. 1873;7(179):417-8. https://doi.org/10.1038/007417a0.
-
21.
Redish AD. Beyond the cognitive map: from place cells to episodic memory. MIT Press Cambridge, MA; 1999.
-
22.
McNaughton BL, Barnes CA, Gerrard JL, Gothard K, Jung MW, Knierim JJ, et al. Deciphering the hippocampal polyglot: the hippocampus as a path integration system. J Exp Biol. 1996;199(Pt 1):173-85. [PubMed ID: 8576689].
-
23.
Whishaw IQ, McKenna JE, Maaswinkel H. Hippocampal lesions and path integration. Curr Opin Neurobiol. 1997;7(2):228-34. https://doi.org/10.1016/s0959-4388(97)80011-6.
-
24.
Marcus GF. The algebraic mind: integrating connectionism and cognitive science. Cambridge: MIT Press; 2001.
-
25.
Gentner D. Why we're so smart. In: Gentner D, Goldin-Meadow S, editors. Language in mind: advances in the study of language and thought. Cambridge: MIT Press; 2003. p. 195-235.
-
26.
Urcelay GP, Miller RR. On the generality and limits of abstraction in rats and humans. Animal Cogn. 2010;13(1):21-32. [PubMed ID: 20012121]. https://doi.org/10.1007/s10071-009-0295-z.
-
27.
Watrous AJ, Lee DJ, Izadi A, Gurkoff GG, Shahlaie K, Ekstrom AD. A comparative study of human and rat hippocampal low-frequency oscillations during spatial navigation. Hippocampus. 2013;23(8):656-61. [PubMed ID: 23520039]. https://doi.org/10.1002/hipo.22124.
-
28.
Piaget J. Behavior and evolution. New York: Pantheon Books; 1978.
-
29.
Meltzoff AN, Moore MK. OBJECT REPRESENTATION, IDENTITY, AND THE PARADOX OF EARLY PERMANENCE: Steps Toward a New Framework. Infant Behav Dev. 1998;21(2):201-35. [PubMed ID: 25147418]. https://doi.org/10.1016/S0163-6383(98)90003-0.
-
30.
Meltzoff AN, Williamson RA, Marshall PJ. Developmental Perspectives on Action Science: Lessons from Infant Imitation and Cognitive Neuroscience. In: Prinz W, Beisert M, Herwig A, editors. Action science: Foundations of an emerging discipline. Cambridge: MIT Press; 2013. p. 280-306. https://doi.org/10.7551/mitpress/9780262018555.003.0011.
-
31.
Kuhn TS. Structure of Scientific Revolutions. Chicago: University of Chicago Press; 1962.
-
32.
Davis H. Transitive inference in rats (Rattus norvegicus). J Comp Psychol. 1992;106(4):342-9. [PubMed ID: 1451416].
-
33.
MacLean EL, Matthews LJ, Hare BA, Nunn CL, Anderson RC, Aureli F, et al. How does cognition evolve? Phylogenetic comparative psychology. Animal Cogn. 2012;15(2):223-38. [PubMed ID: 21927850]. https://doi.org/10.1007/s10071-011-0448-8.